Definición de correlación negativa
En términos simples, la correlación negativa es una relación entre dos variables. Son parte de una función en la que las variables dependientes e independientes se mueven en diferentes direcciones en términos de valor. Por ejemplo, si la variable independiente aumenta, la variable dependiente disminuye y viceversa.
La correlación negativa se puede describir mediante el coeficiente de correlación cuando el valor de esta correlación está entre 0 y -1. La cantidad de una correlación negativa perfecta es -1. La fuerza de la correlación entre las variables puede variar. Por ejemplo, suponga que dos variables, xey se correlacionan con -0,8. Significa que, a medida que x aumenta en 1 unidad, y disminuirá en 0,8. Ahora considere que la correlación negativa entre estas variables es -0,1. En este caso, cada cambio de unidad en el valor de la variable x resultará en una diferencia de 0.1 unidad solo en el costo de la variable y.
Comprender la correlación negativa
Para comprender mejor la correlación negativa, también necesitamos tener una comprensión básica de la correlación. La correlación es una herramienta estadística que mide el grado de relación entre dos funciones diferentes. Por ejemplo, el peso y la altura de una persona. Generalmente, a medida que aumenta la altura, el valor de la persona también aumenta. Indica que hay una correlación positiva entre la altura y el peso porque a medida que aumenta una variable, también aumentan otras variables. Pero la correlación es negativa si las dos variables se mueven en direcciones opuestas, por ejemplo, la altura desde el nivel del sello y la temperatura. A medida que aumenta la altura, la temperatura disminuye.
La fórmula da correlación:

Aquí,
- r = coeficiente de correlación;
- = Media de la variable X;
- = Media de la variable Y
El reordenamiento nos da esta fórmula:

La correlación puede tomar cualquier valor entre -1 y 1. El signo negativo indica una correlación negativa, mientras que un signo positivo indica una correlación positiva. La correlación cero significa que no hay relación entre las dos variables.

¿Por qué es importante la correlación negativa?
- Gestión de carteras : La correlación se utiliza ampliamente en la gestión de carteras. A menudo se dice que las carteras deben ser diversas. Debe consistir en múltiples inversiones que involucren diferentes riesgos y retornos. Si tenemos el mismo tipo de valores en nuestra cartera, cualquier evento importante afectará no solo a un valor, sino a toda la cartera. Para ello, encontramos una correlación entre los rendimientos de los valores. Los depósitos con correlaciones perfectamente positivas no deben comprarse juntos. Para diversificar la cartera, a menudo, se agregan las apuestas con correlaciones negativas. Considere el ejemplo mencionado anteriormente de las acciones de las aerolíneas y los precios del petróleo. Si una cartera tiene acciones de energía, la gerencia puede considerar comprar acciones de aerolíneas para protegerse contra la caída de los precios del petróleo.
- Economía : muchas tendencias asociadas con la economía implican una correlación negativa. Esta relación entre los movimientos puede ser útil para asuntos relacionados con las políticas económicas. Por ejemplo, desempleo y gasto de los consumidores. En cuanto a los aumentos del gasto, el desempleo disminuye (en general).
Ejemplos de la vida real de correlación negativa
- Precios del petróleo y acciones de las compañías aéreas: el petróleo es una materia prima importante para las compañías aéreas. A medida que aumentan los precios del petróleo, su rentabilidad comienza a disminuir, lo que también se refleja en los precios de sus acciones. Por tanto, muestran una correlación negativa
- Mercado de valores y precios del oro (la mayoría de las veces, no siempre): el oro siempre actúa como una opción de inversión alternativa para los inversores en acciones. Por lo tanto, siempre que el mercado de valores parece estar disminuyendo, los inversores se interesan en invertir en oro y, por lo tanto, los precios del oro comienzan a aumentar.
Ejemplo práctico de correlación negativa
Suponga que dos acciones han proporcionado los siguientes rendimientos anualmente en el período 2011-16:

Considerando la rentabilidad de las acciones de la primera acción como variable 'x' y la de la segunda acción como 'y'.
Cálculo de la variable xy
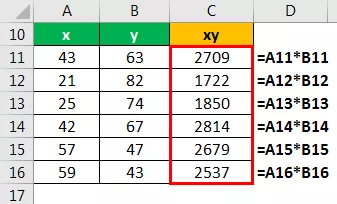
Cálculo de la variable X 2

Cálculo de la variable Y 2

Suma

Cálculo del coeficiente de correlación (r)

- = ((6 * 14311) - (247 * 376)) / (((6 * 11409) - (247 2)) 0.5 * ((6 * 247160- (376 2)) 0.5)
- = Coeficiente de correlación (r) = -0,97608
Consulte la hoja de Excel proporcionada anteriormente para obtener un cálculo detallado.
El valor negativo del coeficiente de correlación muestra que las variables están correlacionadas negativamente.
Conclusión
En ocasiones, puede haber otros factores involucrados que provoquen que las variables se comporten de una manera particular. En el ejemplo discutido anteriormente, se puede deducir que cuando x aumenta, y disminuye. Pero será erróneo suponer que el aumento de 'x' está provocando que la 'y' disminuya porque es posible que ambas empresas en cuestión estén involucradas en negocios completamente diferentes y se vean afectadas por diferentes condiciones económicas.
Por lo tanto, las correlaciones deben usarse solo para determinar una causa. Los ejecutivos pueden usarlo para comprender la relación entre variables, como la demanda del mercado y el gasto del consumidor, que ya existe como parte del análisis. Pero no debe usarse para investigar el cambio en una variable debido a otras variables porque siempre habrá múltiples factores que impacten esa relación. Por ejemplo, el gasto del consumidor en el mercado y los ingresos de una empresa de bienes de consumo. Pueden mostrar una correlación positiva, pero es posible que los ingresos de esa empresa aumentaran debido a alguna otra razón, como el lanzamiento de un nuevo producto o la expansión a una economía emergente.








